Lesson6

scikit-learnの使い方（機械学習）

1. 学習の目標

ここでは scikit-learn というライブラリを利用します。

今まで学んだPythonの知識とscikit-learnというライブラリを活用して、簡単な機械学習のプログラムを構築します。

機械学習の概要
機械学習の流れ
scikit-learnの使い方

2. 機械学習の概要

まずは機械学習とはどういうものかについて学びましょう。機械学習に関する、さまざまな用語を紹介します。

2.1 AI（人工知能）

機械学習が注目された要因のひとつが AI（Artificial intelligence：人工知能） です。AIは、高速な計算処理ができ、さらに人間との対話を行えるコンピュータ（プログラム）です。ひと昔前までは、AIを目にするのはSFの映画やドラマの中だけでしたが、現在は「スマートスピーカー」をはじめ商業施設の店頭で応対するロボットなど、いたるところでAIを利用した技術を見るようになりました。

2019年現在、人間の知能と比較するとAIはまだまだで、発展途上の技術です。それでも、人間の話す言葉を認識して適切な情報を教えてくれたり、車が自動でブレーキを踏んでくれたりと、AI技術の実用化も進んでいます。

2.2 シンギュラリティ（技術的特異点）

現時点のAI技術では実用化できる範囲は限定的ですが、技術が発達し、人間と同等の知能をAIが得たときのことを考えると不安になる人も多いかもしれません。AIが人間を支配するという、SF映画で描かれてきたような世界が現実になる可能性はゼロではないでしょう。

人間の知能にAIが追いつくことを シンギュラリティ（技術的特異点） といいます。AIを研究するレイ・カーツワイル氏が提唱した概念です。シンギュラリティに到達したとき、人間の社会がどのようになるかは誰も予測できない現状で、研究者の間でも一種の問題として考えられています。この問題は、シンギュラリティに到達するのが2045年であると考えられていることから「2045年問題」と呼ばれることもあります。

AI技術を進化させるとともに、AIをどのように制御するかも検討されていかなければなりません。

2.3 機械学習

AI技術の根幹にあるのが 機械学習（machine learning） です。「機械」が「学習」するという言葉のとおり、コンピュータが膨大な数のデータを覚え、それを基にして、ひとつの判断を下すのです。

ここでいう「判断」は、以下のような内容を指します。

人間が写真を見て「これは○○の写真だ」というように「答えが決まっていること」に対してコンピュータが正確に判断すること
「答えがない」ことに対して「将来こうなるのではないか」とコンピュータが予測を立てること
ペットが芸を覚えるときのように「良い行動に報酬を与える」ことで、瞬間瞬間での最良の判断を繰り返すこと

2.4 深層学習（ディープラーニング）とニューラルネットワーク

「機械学習」とは別に 深層学習（ディープラーニング：deep learning） という言葉を見聞きした人も多いかもしれません。機械学習と深層学習は何が違うのでしょうか。それを見ていく前に ニューラルネットワーク（neural network） という言葉について説明します。

単に「機械学習」といっても、コンピュータの学習を実現する仕組みは各種存在します。そのひとつがニューラルネットワークです。ニューラルネットワークは簡単に言うと、人間の脳の構造をコンピュータプログラムで実現した仕組みです。人間の脳は多数の神経回路（ニューロン：neuron）で構成されており、ニューロンとニューロンが繋がることで大きな神経回路を形成しています。外から受けた情報は電気信号として神経回路の中を流れていく仕組みになっていて、新しいニューロンや繋がりができることで人間は新しいことを学習できるのです。

人間の脳（神経回路）の仕組みをコンピュータプログラム上で模しているので「ニューラル」という言葉をつけて「ニューラルネットワーク」と呼んでいます。ニューラルネットワークを利用してコンピュータに学習させるのが「深層学習」です。

つまり、深層学習は機械学習の一部だと思ってください。

ニューラルネットワークや深層学習の仕組みを覚えるのは非常に大変です。深層学習をやってみるだけでしたら「Tensorflow」や「Keras」というPythonのライブラリを導入することで簡単に行えます。とはいえレベルの高い話になるため、本カリキュラムでは深層学習までは扱いません。このレッスンを最後まで学習したあとで、興味の出た方は、ぜひ深層学習についても学んでください。

2.5 教師あり学習と教師なし学習

機械学習では、ひとつの判断を下すために利用する大量のデータをどのように使って学習するのでしょうか。

その方法は2つあります。教師あり学習 と 教師なし学習 です。

2つの違いは、簡単に言えば「答えがあるかないか」です。学習させるデータに答えがある場合「教師あり学習」、答えのない場合が「教師なし学習」となります。

先述の事例で言えば、写真をみて「これは○○の写真だ」と判断する場合は教師あり学習を使います。何の写真かわからない状態で写真を覚えさせられても、判断の材料にならないからです。

これとは別に、将来予測では教師なし学習を使います。実測値を学習した上で傾向を分析し、その分析結果を基に「○○の値がこうなら、△△の値は、こうなるのではないか」と予測を立てるのです。なお、同じ予測でも、たとえば「年齢、性別、職業などの情報と喫煙の有無」が記録されたデータを学習して「この年齢・性別・職業なら喫煙しているのではないか」と予測を立てるのは教師あり学習に該当します。

2.6 強化学習

ペットに芸を教えるという一種のたとえを先ほど書きましたが、教師あり学習や教師なし学習とは違い、試行錯誤を繰り返す中で「より良い行動をしたら報酬を得られる」というルールで学習を続けていき、瞬間瞬間での最良な判断を繰り返していく手法が 強化学習 です。

強化学習は将棋やチェスをするAIで活用されています。最初は、インターネット上に存在する大量の棋譜を「教師あり学習」で学習させますが、学習が完了したAI同士を対局させ、その中で強化学習を行う（より良い手を打ったら報酬を与える）ことでAIの能力を高めていきます。また、テレビゲームをAIにプレーさせる中で、より前へ進む行動に報酬を与える形で強化学習を行い、ステージクリアを目指すということに挑戦している方もいます。その様子を動画サイトで公開されていることもありますので、興味ある方は視聴してみると、おもしろいでしょう。

2.7 分類と回帰

学習したAIが教えてくれること（データを分析する方針）は分類と回帰の2つに分けられます。

分類

「これは○○の写真だ」と判断するのは分類に該当します。「いくつかある選択肢の中のどれになるか」はっきりと答えを言うのが分類だと思ってください。

データを解析して捉えた特徴を基にして「これは○○だ」と分類します。

回帰

それに対して「施設の利用回数」や「価格」など、連続的な数値について予測するのが回帰です。

回帰では統計学の知識や計算を使います。データを数学的な関数の式やグラフに当てはめて分析し、法則を導き出します。

2.8 scikit-learnの概要

このレッスンでは機械学習を体験するために scikit-learn というパッケージライブラリを利用します。

Pythonでは機械学習や深層学習を行う上で便利なライブラリが数多く存在しています。その中でもscikit-learnは機械学習のほとんどの分野をカバーしている汎用性を持ち、さらに機械学習の初心者でも使いやすい特徴があるため、非常に人気のライブラリです。

機械学習の特定の分野についてプログラムを作りたい場合は、他のライブラリの導入を検討した方が良い場合もあります。たとえば深層学習なら「Tensorflow」や「Keras」です。しかし、機械学習そのものが初体験という方には扱い方が難しいものも多いので、最初はscikit-learnで簡単なレベルの機械学習を学んでから、他のライブラリや特定分野の学習へステップアップすることをオススメします。

3. 機械学習の流れ

Pythonで機械学習プログラムを作る際の、大まかな流れは、次の通りです。

モデルを決める
学習に使うデータセットをインポートする
データの前処理をする
データを訓練データ（train data）とテストデータ（evaluate data）とに分ける
モデルを作って学習する
期待する性能が出たかを評価する

6_03_01

3.1 モデルを決める

機械学習で処理するロジックのことを「モデル（model）」と言います。独自のモデルを作ることもできますが、scikit-learnには、さまざまなモデルが提供されており、最初はそのなかから選ぶとよいでしょう。

scikit-learnで提供されているチートシートを見ると、どれを選べばよいのか、大まかにわかります。

Choosing the right estimator | scikit-learn documentation

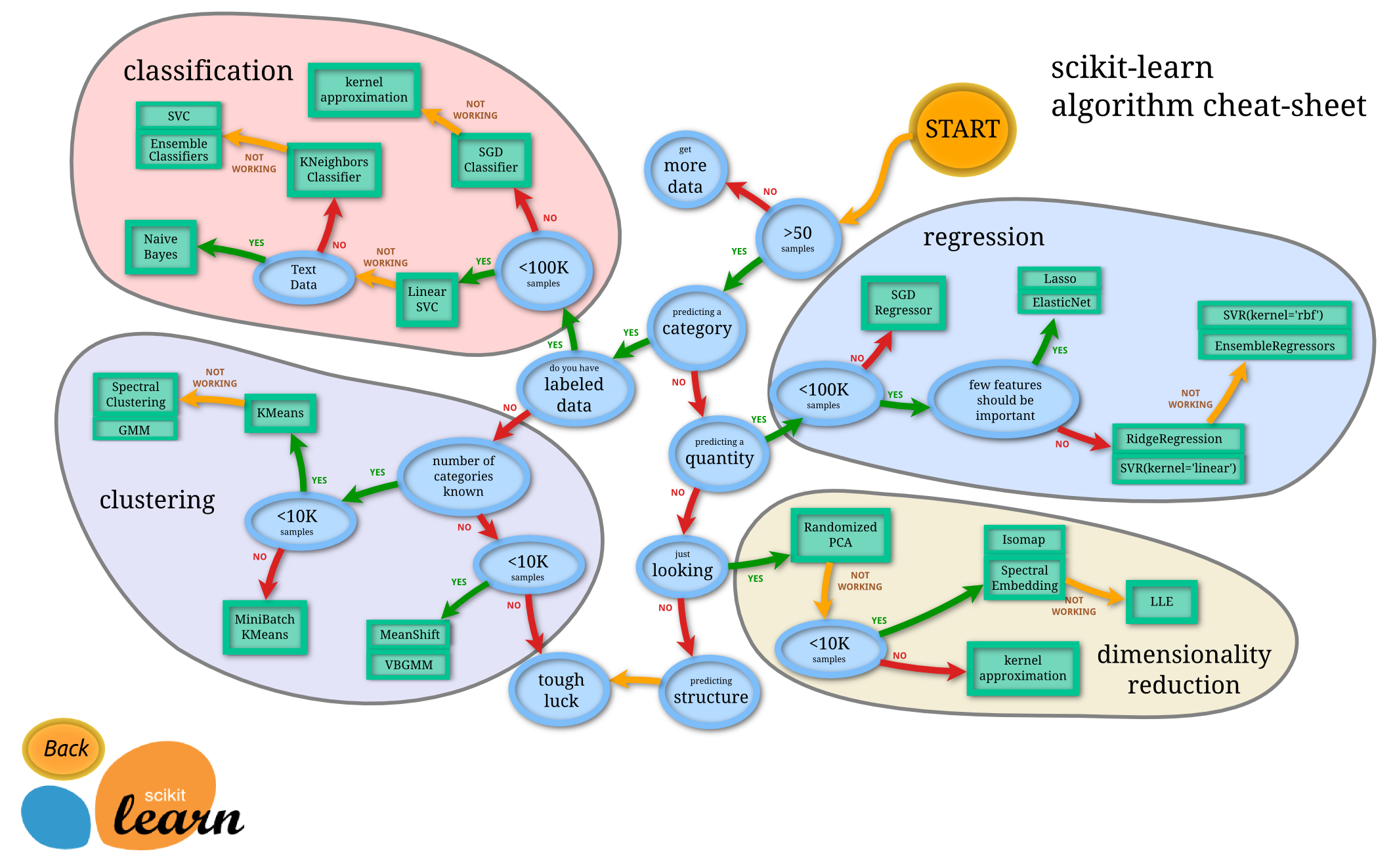
scikit-learn algorithm cheat-sheet

scikit-learn algorithm cheat-sheet(引用元：上記のscikit-learn公式のページより)

チートシートでは、大きく4つのグループに分かれています。まずは、何をしたいかによってグループを選び、それから、その分類のなかにあるモデルのなかからひとつを選びます。ときには、こうしたモデルを多段に組み合わせることもあります。

① 回帰（regression）

連続したデータから、その傾向を出力する連続値を出力します。たとえば過去の実績から未来の数値を予測するなどです。教師あり学習です。

② 分類（classification）

データを分類します。たとえばメール本文を入力として迷惑メールか否かを決めたり、手書き文字が何の文字か分類するなどです。教師あり学習です。

③ クラスタリング（clustering）

データの類似性によって、グループ化します。たとえば顧客の購買データを入力して、似ている傾向の顧客を集めるなどです。そうすればリコメンド（他のオススメ商品を紹介する）に使えます。ほかの例としては、たとえば「人物」「車」「山」「川」など、さまざまなシチュエーションの写真がたくさんあるとき、似たような写真でグループ化することなどもできます。教師なし学習です。

④ 次元削減（dimensionality reduction）

データの特徴量を捕らえて、より小さなデータ量に削減します。多数の項目からなるデータを処理する際、それを直接使うと計算量が多くなるときなどに必要となります。次元圧縮とも呼ばれます。教師なし学習です。

3.2 学習に使うデータセットをインポートする

モデルを決めたら、機械学習のプログラムを作っていきます。

最初に、学習に使うデータを取り込みます。機械学習の勉強のためであれば、scikit-learnで最初から用意されているサンプルデータを使うとよいでしょう。

ここでは、機械学習でよく使われる「アヤメ（iris）」のサンプルデータを読み込んでみます。

                    from sklearn import datasets
irisdata = datasets.load_iris()

scikit-learnに含まれるサンプルデータは、その書式やデータの意味が DESCR プロパティに記載されています。次のようにして確認できます。

print(irisdata.DESCR)

出力結果：

                    .. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica

    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988
…略…

                  

「Sepal Length（がく片の長さ）」「Sepal Width（がく片の幅）」「Petal Length（花びらの長さ）」「Petal Width（花びらの幅）」の4つのデータが irisdata の dataプロパティに格納され、それらが「Setosa」「Versicolor」「Virginica」のどの品種に属するかが irisdata の target プロパティに格納されています。target には Setosa Versicolor Virginica の文字列そのものではなく、0 1 2 の整数値が入っています。これは、Setosa = 0, Versicolor = 1, Virginica = 2 を意味しています（カテゴリ値：詳細は後述）。

「アヤメに関する4つの長さ」のように、それぞれがどういう特徴を持っているかを説明するデータを 説明変数 や 特徴量 、また「アヤメのカテゴリ値」のように、それが何の種類に属しているかを示すデータを 目的変数 といいます。

scikit-learnに含まれるサンプルデータは data プロパティに説明変数（特徴量）が、target プロパティに目的変数が入っています。

print(irisdata.data)

出力結果：

[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]
 [5.4 3.9 1.7 0.4]
 …略…]

print(irisdata.target)

出力結果：

                    [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2]

                  

targetは、このように「0」「1」「2」のいずれかの値になっており、「Setosa」「Versicolor」「Virginica」のそれぞれに対応します。

data と target は、それぞれ配列（ndarray）です。shape プロパティを参照することで、配列の要素数がわかります。

                    print(irisdata.data.shape)
print(irisdata.target.shape)

出力結果：

                    (150, 4)
(150,)

data は 縦150行 x 横4列 の配列、 target は 縦150行 x 横1列 の配列です。data と target は番号（添字）の同じ要素がペアとなっています。たとえば、0番目の要素の data（説明変数）である [5.1 3.5 1.4 0.2] に対応する target（目的変数）は、同じ0番目の要素である 0 となります。

data の横の列がそれぞれ何のデータか、また、target の値 0,1,2 がそれぞれ何を表しているかは、以下のプロパティを参照するとわかります。

                    print(irisdata.feature_names)
print(irisdata.target_names)

出力結果：

                    ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
['setosa' 'versicolor' 'virginica']

3.3 データの前処理を行う

インポートしたデータは、そのまま使えるとは限りません。計測データの場合、ノイズや誤差があったり、値がうまくとれていないことがあります。また正しいデータであっても、説明変数間の単位が大きく違うと、適切に学習できないことがあります。そこで必要になるのが、データの 前処理 です。

前処理は、学習しやすいようにする、さまざまな加工です。目的によって異なりますが、たとえば、次のようなものがあります。

カテゴリ値の数値化

機械学習では、数値を扱います。たとえば「ネコ」「イヌ」「風景」のカテゴリに分類するモデルを作る場合、この文字を扱うのではなく ネコ = 0, イヌ = 1, 風景 = 2 のように数値化します。このように数値化されたデータを カテゴリ値 といいます。

ここでのアヤメのサンプルの場合は、すでに Setosa = 0, Versicolor = 1, Virginica = 2 のようになっていますが、自分でデータを作る場合は、こうした数値化をしなければなりません。

ダミー変数化

カテゴリ値の数値化とも関連しますが、機械学習の計算方式（アルゴリズム）によっては、テストの点数のように「数値の大小に意味がある」という認識となってしまい、適切に学習できないことがあります。今回のアヤメの例であれば、Setosa（0）よりVirginica（2）のほうが優位にあるものと認識される場合があります。そのようなときは、横軸に項目名を持ち、「0」か「1」かを持つ変数マトリックスに展開するように分解します。これを ダミー変数 と言います。ダミー変数化が必要かどうかは、学習データの性質によります。

ダミー変数化前

カテゴリの値	値
Setosaのとき	0
Versicolorのとき	1
Virginicaのとき	2

ダミー変数化後

値・列名	Setosa	Versicolor	Virginica
Setosaのとき	1	0	0
Versicolorのとき	0	1	0
Virginicaのとき	0	0	1

また、以下のように、列を1つ減らして「すべての列が0だったらVirginicaとする」という処理を行ったほうが、精度向上を見込める場合もあります。

値・列名	Setosa	Versicolor
Setosaのとき	1	0
Versicolorのとき	0	1
Virginicaのとき	0	0

列をひとつ減らすのは必須の対応ではありませんが、ダミー変数の列どうしに強い関係性が発生し、学習精度に悪い影響を与えている場合に効果的です（このようなケースを多重共線性といいます）。

欠損データの補完（穴埋め）

データが一部欠損している場合、 補完（穴埋め） することを検討します。それを「0」として扱うのか、「前後の平均で補完するか」、そもそも、全部を捨ててしまうか、などを決めます。

単純に0にすると実際のデータと大きくかけ離れるので、ほとんどの場合、そうすることはありません。全部捨ててしまうのはよい方法ですが、そうするとデータ数が足りなくなって、十分な学習ができないかも知れません。また前後の平均で補完する方法もよく使われますが、誤差を大きくするかもしれません。

ですから、どの方法がよいのかは、一概に言えません。データの性質や量、目的によって、選択する必要があります。

なお、ここでサンプルとして読み込んだアヤメのデータの場合、DESCRプロパティにはMissing Attribute Values: Noneと記述されており、欠損値はありません。

スケーリング

ある列の数値の範囲（上限と下限）が、ほかの列と大きくかけ離れる場合、その列が少し変わっただけで、全体に大きく影響を与える可能性があります。

そこで必要なのが スケーリング です。スケーリングとは、各列の数値データの範囲を、およそ0〜1（もしくはマイナス1〜1）の範囲に収められるように再計算することをいいます。

どのようなモデルを作るのかにもよりますが、各列の数値の範囲が、大きく違う場合は、スケーリングするのがよいでしょう。

情報保護に関連する加工（マスキング）

機械学習では、個人情報を扱うこともあります。就活生の内定辞退を予測するサービスが大きな問題となったように、個人情報を「機械学習が学習して判断した結果」によって、自分の情報が公に晒されたり、知らないところで悪意のあるレッテルを貼られたりすることも考えられます。

そういうときには、個人を特定する部分を隠す マスキング などの処理をします。

画像や音声を処理しやすくする加工

画像や音声を取り扱う場合は、学習しやすいように加工します。データの量が少ないほど学習にかかる時間が少なくて済みますが、細部が潰れて学習に影響を及ぼすこともあるので、目的によって適切に調整します。

画像の場合は、ノイズを除去したり、一部を切り出したり、傾きを補正したりしたほうが良い結果を得られることもあります。さらに、色の情報が必要ないときは、 グレースケールにする のも有効です。

音声についても同じです。

データの水増し

一般にデータをたくさん用意できたほうが、学習効果が高まります（ただし学習させ過ぎると、その学習データに特化した結果が出やすくなり、汎用的になりにくくなるという別の問題が生じます）。どうしてもデータが足りない場合、学習の際に 水増し をすることもあります。

画像の場合は、拡大や縮小、回転、反転などの幾何学操作をしたり、ノイズを加えたりした画像を作ることで水増しします。とくに、多くの学習データが必要な深層学習のような学習では、よく使われるテクニックです。

3.4 データを訓練データとテストデータに分ける

機械学習ではデータを 訓練データ と テストデータ とに分けます。訓練データはコンピュータに覚えさせたいデータ、テストデータは学習結果の正確さを検証するために使うデータです。

訓練データとテストデータの分け方には、単純に「○番目から△番目までのデータを訓練データ、それ以降をテストデータ」と分ける方法の他、ランダムに振り分ける方法、などがあります。インポートしたデータが規則順に並んでいるときに単純な2分割を行うと、訓練データに偏りが生じるので、極力ランダムに振り分けられると良いでしょう。

すべてのデータを訓練データとテストデータに分ける際、テストデータは全体の2割から3割程度で振り分けるのが望ましいです。訓練データが少なすぎると判断材料が少ないため、精度が悪くなるのは想像に難くありませんが、多すぎても思考の癖が生じてしまい、判断の精度が落ちてしまう可能性があります。このような状態を 過学習 といいます。

過学習を防ぐ方法は複数ありますが、テストデータの割合を考慮するだけでも充分な精度が望めます。

なおscikit-learnでプログラミングする場合は説明変数を X 、目的変数をy とし、さらに訓練データには _train 、テストデータに _test という文字列を変数名に付け加えるのが慣例です。ランダムに振り分けるなら、scikit-learnの train_test_split() を使うのが便利です。以下に一例を示します。

                    from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(irisdata.data, irisdata.target, test_size = 0.2, train_size = 0.8, shuffle = True)

train_test_split()で

shuffle =
                  True

（分割前にランダムな並び替えを行う）というキーワード引数を指定しているため、以降の実習内容において、皆さんの実行結果がカリキュラムに掲載のものと少し異なる結果になる可能性があります。エラーが出ない限りは正常に処理が実行できていると考えて、学習を進めてください。

3.5 モデルを作って学習する

ここまでが、機械学習の前処理だと思ってください。次に、機械学習モデルを作って学習します。

scikit-learnには、代表的な機械学習モデルがあるので、インポートして簡単に作れます。ここでは、比較的高い精度を得られる「サポートベクトル」を利用した分類モデル（SVC）を使います。

たとえば、サポートベクトルの分類モデルの中でも「線形分類モデル」を作るには、次のようにします。gamma="scale" のキーワード引数は、指定しないと警告の表示が出るための対処だという理解で問題ありません。

                    from sklearn.svm import SVC

classifier = SVC(kernel = "linear", gamma = "scale")

作ったモデルの fit メソッドを実行すると、学習が実行されます。

classifier.fit(X_train, y_train)

出力結果：

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='scale',
    kernel='linear', max_iter=-1, probability=False, random_state=None,
    shrinking=True, tol=0.001, verbose=False)

3.6 期待する性能が出たかを評価する

以上で、機械学習モデルができました。分けて残して置いたテストデータを predict メソッドで、この学習済みモデルに入れて、モデルの評価を実行します。

y_pred = classifier.predict(X_test)

ここで求めた y_pred が機械学習によって求められた結果です。

print(y_pred)

出力結果の一例：

[1 1 2 1 2 2 0 2 1 1 0 2 0 1 0 2 1 2 1 0 0 1 2 0 0 2 2 2 1 0]

テストデータの元々の結果である y_test とどれだけ合致しているかを見て、モデルの性能を評価したいのですが、ひとまず y_test をそのまま表示してみます。

print(y_test)

出力結果の一例：

[1 1 2 1 2 2 0 2 2 1 0 2 0 1 0 2 2 2 2 0 0 1 2 0 0 2 1 2 1 0]

少し横に伸びていて見にくいので、集計した結果で y_pred と y_test の合致度（モデルの性能）を評価します。

性能を測る方法は、いくつかあり、たとえば accuracy_scoreを使って、正答率を見る方法があります。

                    from sklearn import metrics

print(metrics.accuracy_score(y_test, y_pred))

出力結果の一例：

0.8666666666666667

上記の例では、正答率は、86.67%のようです。

他にも 混同行列 というものを表示する方法があります。以下のような表示内容が混同行列です。

print(metrics.confusion_matrix(y_test, y_pred))

出力結果：

[[ 9  0  0]
 [ 0  7  1]
 [ 0  3 10]]

これをどう見るか、ですが、縦の並び（行）が「正解」、横の並び（列）は「分類器が出力した結果」です。簡単に言うと 左上から右下に引いた対角線上の数値が正解数 になります。

上記の混同行列では、分類器が不正解だったデータは4つだけ、ということになります。

正答率を表示する、もうひとつの方法があります。classification_report() を実行してください。

print(metrics.classification_report(y_test, y_pred))

出力結果：

             precision    recall  f1-score   support

          0       1.00      1.00      1.00         9
          1       0.70      0.88      0.78         8
          2       0.91      0.77      0.83        13

avg / total       0.88      0.87      0.87        30

recall の列が正解率です。全体の正解率が 0.87（87％）ということで、良い精度の分類器が作成されたと言えます。

以上が集計方法の一例です。Matplotlibでグラフ化して評価する方法も良いでしょう。

4. scikit-learnの使い方

事例をとおして、scikit-learnの使い方を学びましょう。

4.1 実践1：手書き数字の画像の分類

最初に画像の分類プログラムを作ってみましょう。

ここではscikit-learnが持っている手書き数字のサンプル画像を利用して、それが何の数字が描かれた画像かを分類します。

使用するモデルについて

分類の機械学習を行いたいので、今回も SVC の線形分類モデルを使います。

学習に使うデータセットをインポートする

JupyterLabで新規ノートブックを作成し、タイトルを Lesson6_1_digits としてください。

まずはscikit-learnと手書き数字のサンプルデータセットをインポートしましょう。

                    from sklearn import datasets
digits = datasets.load_digits()

データセットの概要は DESCR プロパティで確認できます。

print(digits.DESCR)

出力結果：

Optical Recognition of Handwritten Digits Data Set
===================================================

Notes
-----
Data Set Characteristics:
    :Number of Instances: 5620
    :Number of Attributes: 64
    :Attribute Information: 8x8 image of integer pixels in the range 0..16.
    :Missing Attribute Values: None
    :Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
    :Date: July; 1998

This is a copy of the test set of the UCI ML hand-written digits datasets
http://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits

The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.

Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.

For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.

References
----------
  - C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
    Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
    Graduate Studies in Science and Engineering, Bogazici University.
  - E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
  - Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
    Linear dimensionalityreduction using relevance weighted LDA. School of
    Electrical and Electronic Engineering Nanyang Technological University.
    2005.
  - Claudio Gentile. A New Approximate Maximal Margin Classification
    Algorithm. NIPS. 2000.

いったん data と target をそれぞれ X と y に分けておきます。

                    X = digits.data
y = digits.target

配列の大きさ（データの個数）を調べてみます。

                    print(X.shape)
print(y.shape)

出力結果：

(1797, 64)
(1797,)

1797個のデータがあります。今回の計測データ X の shape で表示された 64 は、データが 8ピクセル × 8ピクセル の画像データ（モノクロ画像）になっていることを表します。各ピクセルのデータは白黒の度合いを16段階の数値にしています。画像データの配列仕様について忘れてしまった方は「Pillow」のレッスンを再度復習してください。

なお、画像データに対して「計測」という言葉を使うのは変かもしれませんが、レッスン全体で共通した形で話を進めたいので、ここでも「計測データ」と呼びます。

データの中身を見てみましょう。

                    print(X[0])
print(y[0:50])

出力結果：

[ 0.  0.  5. 13.  9.  1.  0.  0.  0.  0. 13. 15. 10. 15.  5.  0.  0.  3.
 1.   2.  0. 11.  8.  0.  0.  4. 12.  0.  0.  8.  8.  0.  0.  5.  8.  0.
  1.  9.  8.  0.  0.  4. 11.  0.  1. 12.  7.  0.  0.  2. 14.  5. 10. 12.
  2.  0.  0.  0.  6. 13. 10.  0.  0.  0.]
[0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 5 5 6 5 0
 9 8 9 8 4 1 7 7 3 5 1 0 0]

データの構造はわかりました。でも、せっかくなので、どういう手書き画像になっているかを画面に表示してみましょう。最初の10件が0から9まで順番どおりに並んでいるようなので、それらを表示します。

                    import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()

for i, x in enumerate(X[0:10], 0):
    sp = fig.add_subplot(2, 5, (i + 1))
    sp.imshow(x.reshape(8, 8), cmap = "gray")

                  

出力結果：

データの前処理について

今回のサンプルは、とくに前処理の必要がないサンプルデータとなっています。前処理についてはスキップして、データの分割を行います。

データを訓練データとテストデータに分ける

今回の手書き数字のデータは順序よく並んではいないようなので、単純に「○○○件目で区切る」方法を使うので問題ありません。

このテストデータは1800件弱ほどありますので、今回は1200件目までを訓練データ、1201件目以降をテストデータとしてください。

                    X_train = X[:1201]
X_test  = X[1201:]
y_train = y[:1201]
y_test  = y[1201:]

                  

また、各ピクセルのデータはすべて16段階で表現したデータになっているため、スケーリングも必要ありません。

モデルを作って学習する

今回も線形分類器を使って分類器を作成しましょう。

                    from sklearn.svm import SVC
classifier = SVC(kernel = "linear", gamma = "scale")
classifier.fit(X_train, y_train)

                  

出力結果：

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='scale', kernel='linear',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)

期待する性能が出たかを評価する

テストデータ X_test を分類器にかけましょう。

y_pred = classifier.predict(X_test)

まずは y_pred と y_test をそのまま表示してみます。

print(y_pred)

出力結果：

[7 3 5 1 0 0 2 2 7 8 2 0 1 2 6 3 3 7 3 3 4 6 6 6 4 9 1 5 0 9 5 2 8 2 0 0 1
 7 6 3 2 1 7 4 6 3 1 3 9 1 7 6 8 4 3 8 4 0 5 3 6 9 6 6 7 5 4 4 7 2 8 2 2 5
 7 9 5 4 8 8 4 9 0 8 9 8 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4
 5 6 7 8 9 0 9 5 5 6 5 0 9 8 9 8 4 1 7 7 3 5 1 0 0 2 2 7 8 2 0 1 2 6 3 3 7
 3 3 4 6 6 6 4 9 1 5 0 9 6 2 8 2 0 0 1 7 6 3 2 1 7 4 6 3 1 3 9 1 7 6 8 0 3
 1 4 0 5 3 6 9 6 1 7 5 4 4 7 2 8 2 2 5 7 9 5 4 8 8 4 5 0 8 0 1 2 3 4 5 6 7
 3 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 5 5 6 5 0 9 8 9 8 4 1 7 7
 3 5 1 0 0 2 2 7 8 2 0 8 2 6 3 3 7 3 3 4 6 6 6 4 9 9 5 0 9 5 2 3 2 0 0 9 7
 6 3 2 9 7 4 6 3 1 3 9 1 7 6 8 4 3 9 4 0 5 3 6 9 6 9 7 5 4 4 7 2 8 2 2 5 7
 9 5 4 8 8 4 3 0 7 9 8 0 1 2 3 4 5 1 7 1 9 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7
 8 9 6 9 5 5 6 5 0 9 4 9 8 4 1 7 7 3 5 1 0 0 0 2 7 8 2 0 1 2 6 8 3 7 7 3 4
 6 6 6 9 9 1 5 0 9 5 2 8 0 1 7 6 3 2 1 7 8 6 3 1 3 9 1 7 6 8 4 3 1 4 0 5 3
 6 9 6 1 7 5 4 4 7 2 2 5 7 8 5 9 4 5 0 8 9 8 0 1 2 3 4 5 6 7 8 9 0 1 2 8 4
 5 6 7 8 9 0 1 2 8 4 5 6 7 8 9 0 9 5 5 6 5 0 9 8 9 8 4 1 7 7 7 5 1 0 0 2 2
 7 8 2 0 1 2 6 8 8 7 5 8 4 6 6 6 4 9 1 5 0 9 5 2 8 2 0 0 1 7 6 3 2 1 7 4 6
 3 1 3 9 1 7 6 8 4 8 1 4 0 5 3 6 9 6 1 7 5 4 4 7 2 8 2 2 5 7 9 5 4 8 8 4 9
 0 8 9 8]

print(y_test)

出力結果：

[7 3 5 1 0 0 2 2 7 8 2 0 1 2 6 3 3 7 3 3 4 6 6 6 4 9 1 5 0 9 5 2 8 2 0 0 1
 7 6 3 2 1 7 4 6 3 1 3 9 1 7 6 8 4 3 1 4 0 5 3 6 9 6 1 7 5 4 4 7 2 8 2 2 5
 7 9 5 4 8 8 4 9 0 8 9 8 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4
 5 6 7 8 9 0 9 5 5 6 5 0 9 8 9 8 4 1 7 7 3 5 1 0 0 2 2 7 8 2 0 1 2 6 3 3 7
 3 3 4 6 6 6 4 9 1 5 0 9 5 2 8 2 0 0 1 7 6 3 2 1 7 4 6 3 1 3 9 1 7 6 8 4 3
 1 4 0 5 3 6 9 6 1 7 5 4 4 7 2 8 2 2 5 7 9 5 4 8 8 4 9 0 8 0 1 2 3 4 5 6 7
 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 5 5 6 5 0 9 8 9 8 4 1 7 7
 3 5 1 0 0 2 2 7 8 2 0 1 2 6 3 3 7 3 3 4 6 6 6 4 9 1 5 0 9 5 2 8 2 0 0 1 7
 6 3 2 1 7 4 6 3 1 3 9 1 7 6 8 4 3 1 4 0 5 3 6 9 6 1 7 5 4 4 7 2 8 2 2 5 7
 9 5 4 8 8 4 9 0 8 9 8 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 9 0 1 2 3 4 5 6 7
 8 9 0 9 5 5 6 5 0 9 8 9 8 4 1 7 7 3 5 1 0 0 2 2 7 8 2 0 1 2 6 3 3 7 3 3 4
 6 6 6 4 9 1 5 0 9 5 2 8 0 1 7 6 3 2 1 7 4 6 3 1 3 9 1 7 6 8 4 3 1 4 0 5 3
 6 9 6 1 7 5 4 4 7 2 2 5 7 9 5 4 4 9 0 8 9 8 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4
 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 9 5 5 6 5 0 9 8 9 8 4 1 7 7 3 5 1 0 0 2 2
 7 8 2 0 1 2 6 3 3 7 3 3 4 6 6 6 4 9 1 5 0 9 5 2 8 2 0 0 1 7 6 3 2 1 7 4 6
 3 1 3 9 1 7 6 8 4 3 1 4 0 5 3 6 9 6 1 7 5 4 4 7 2 8 2 2 5 7 9 5 4 8 8 4 9
 0 8 9 8]

割と近いように思えます。混同行列を見てみましょう。

                    from sklearn import metrics
print(metrics.confusion_matrix(y_test, y_pred))

出力結果：

[[58  0  0  0  0  0  1  0  0  0]
 [ 0 53  0  0  0  0  1  0  2  5]
 [ 1  0 59  0  0  0  0  0  0  0]
 [ 0  0  0 52  0  1  0  2  7  0]
 [ 1  0  0  0 57  0  0  0  1  2]
 [ 0  0  0  0  0 58  1  0  0  0]
 [ 0  1  0  0  0  0 60  0  0  0]
 [ 0  0  0  0  0  0  0 60  0  0]
 [ 0  1  0  2  1  0  0  1 50  0]
 [ 0  0  0  1  0  2  0  1  1 53]]

具体的な数値としての正答率を確認します。

print(metrics.classification_report(y_test, y_pred))

出力結果：

             precision    recall  f1-score   support

          0       0.97      0.98      0.97        59
          1       0.96      0.87      0.91        61
          2       1.00      0.98      0.99        60
          3       0.95      0.84      0.89        62
          4       0.98      0.93      0.96        61
          5       0.95      0.98      0.97        59
          6       0.95      0.98      0.97        61
          7       0.94      1.00      0.97        60
          8       0.82      0.91      0.86        55
          9       0.88      0.91      0.90        58

avg / total       0.94      0.94      0.94       596

上記の例ではrecall（正答率）が 0.94 、つまり94%であると出ました。かなり良い精度の分類器になったようです。

4.2 実践2：ビットコインの価格変動の予測

ここからは回帰の機械学習プログラムを作成していきましょう。まずはビットコインの価格変動データを使って、直近の未来の価格変動を予測するプログラムです。なお、ここではscikit-learnのサンプルデータを使うのではなく、インターネットから入手したCSVファイルをプログラムにインポートしてプログラムを作成します。

使用するモデルについて

今回は分類ではなく予測を行いたいので、回帰のモデルを使います。回帰モデルの場合でも、scikit-learnで用意されている SVR クラスを利用することで、さまざまな回帰モデルを汎用的に作成できます。SVC の場合と同じようにkernel = "linear" というキーワード引数を利用します。

しかし今回は SVR よりも簡単に手軽に線形回帰モデルを作成できる LinearRegression クラスを利用します。流れは SVC や SVR と一緒です。

学習に使うデータセットをインポートする

まずはデータセットをダウンロードします。今回のデータは coincheck というサイトの Bitcoin(USD) price のページから過去にダウンロードしたCSVファイルを利用します。下記の緑色のボタンをクリックし、CSVファイルをダウンロードしてください。

CSVファイルをダウンロードする

coindesk-bpi-USD-close_data-2018-06-07_2018-06-27.csv がダウンロードされました。このCSVファイルには、2018年6月7日から2018年6月27日までの21日間における1時間ごとのビットコイン価格、つまり 21日 × 24時間 = 504件 のビットコイン価格データが保存されています。（※ 現在のcoincheckのサイトでは、同じような「21日間における1時間ごとの価格データ」としてCSVを取得することができないようになっているので、学習を進める際は、必ず上記のボタンからダウンロードしたCSVファイルを活用してください。）

今回作成するプログラムでは、最初にPandasで価格データを読み込む方法でインポートしますので、CSVファイルをCloud9（Lesson6関係のノートブックのファイルが格納されている場所）にアップロードしてください。

CSVファイルをアップロードできましたら、同じフォルダにJupyterLabの新しいノートブックを作成し、名前を Lesson6_2_bitcoin に変更してください。最初のセルに以下の内容を記述し、実行してください。

                    import pandas as pd
btc_price = pd.read_csv('coindesk-bpi-USD-close_data-2018-06-07_2018-06-27.csv')

アップロードできましたら、Pandasが出力するCSVのデータを先頭5件だけ表示してみましょう。

btc_price.head()

出力結果：

回帰の場合でも、学習データを読みこんだら、説明変数 X と目的変数 y に分けておきます。

回帰では y = aX + b のような数学的な関数式にデータを当てはめて分析していきます。

ここでは少し工夫をします。X はPrice、y は 次の時間の Priceとしましょう。つまり「ある時間のPriceが X なら、1時間後 y になる」という形で X （説明変数）と y（目的変数）を設定します。

また、今回のデータは504件ありますが、中途半端なのでキリ良く500件までのデータを使うことにします。以下のコードを記述、実行して、訓練データと教師データに分けてください。

                    X = btc_price.loc[0:499, ["Close Price"]]
y = btc_price.loc[1:500, ["Close Price"]]

データはPriceのみとしたかったのでDate列は省きました。カラム名を指定しての分割を行うためlocを使いました（おさらいですがカラムの位置の数値を指定して分割する場合はilocを使います）。また、y は X から1つ後ろにずらして格納したので、上記のとおり「1時間後のPrice」が入っています。X.head() ならびに y.head() で確認してみると良いでしょう。

出力結果：

データの前処理について

今回のデータも欠損値は無く、スケーリングなどの処理も不要なため、前処理についてはスキップします。

データを訓練データとテストデータに分ける

回帰でも X と y を訓練データとテストデータに分割して、 X_train, X_test, y_train, y_test の配列4つを作成します。

今回は時系列でデータが並んでいるため、ランダムに並び替えると精度に悪い影響が出るかもしれませんので、train_test_split() は使いません。単純に500件あるうちの先頭400件を訓練データ、後ろ100件をテストデータとします。

なお、X と y はPandasの2次元配列形式（DataFrame）であるため、NumPyの配列形式（ndarray）に変換する必要があります。

                    import numpy as np
X_train = np.array(X[:400])
X_test  = np.array(X[400:])
y_train = np.array(y[:400])
y_test  = np.array(y[400:])

                  

※ 今回の X_train は400行 × 1列なので不要ですが、 X_train が1次元配列となっている場合は reshape() などで2次元配列に変える必要があります。

モデルを作って学習する

最初に説明したとおり、手軽に線形回帰モデルを作成できる LinearRegression クラスを利用します。

以下のコードを記述、実行してください。

                    from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X_train, y_train)

                  

これで線形回帰モデルが作成できました。

期待する性能が出たかを評価する

回帰の場合でも、テストデータを基に予測を実施するときは predict() メソッドを利用します。

y_pred = model.predict(X_test)

回帰モデルから導き出した予測値が y_pred に、実際の値（正解）が y_test に入っています。まずは、そのまま出力してみます（出力結果の数値は一例です）。

print(y_pred)

出力結果の一例：

[[6122.0451564 ]
 [6140.09481289]
 [6133.60527174]
 [6149.12460256]
 [6135.21277276]

...（中略）...

 [6111.16971741]
 [6123.16643797]
 [6122.20392193]
 [6120.5071153 ]
 [6144.79824179]]

print(y_test)

出力結果の一例：

[[6139.12]
 [6132.58]
 [6148.22]
 [6134.2 ]
 [6237.66]

...（中略）...

 [6122.06]
 [6121.09]
 [6119.38]
 [6143.86]
 [6127.15]]

これだけだと正確なのか不明です。また、今回は分類ではなく予測を行っているので、accuracy_scoreを用いてモデルの評価を行うのは適切ではありません。

そこで、今回は、予測値と実際の値をグラフに重ねて表示してみましょう。

                    %matplotlib inline
import matplotlib.pyplot as plt
plt.plot(range(0,100), y_test, label='Actual price', color='blue')
plt.plot(range(0,100), y_pred, label='Predicted price', color='red')
plt.xlabel('Hours')
plt.ylabel('Price ($)')
plt.title('Bitcoin Price')
plt.grid(True)
plt.legend(loc = "upper left")

                  

出力結果の一例：

青い線が実際の値、赤い線が予測値です。上記の例では、ほぼ同じようなグラフの線になっており、精度の良い予測ができています。

5. まとめ

このレッスンでは2つの機械学習プログラムを作成してもらいました。分類の機械学習と回帰の機械学習を両方とも体験していただきました。

今回の内容を踏まえて、さらなる機械学習の勉強に役立ててください。

Lesson7 機械学習の実践へ進む